Referencja nr 3.
Rozwiązanie pokazuje konstrukcję geometryczną niezbędną do obliczenia kąta skręcenia osi długich dwóch elips powstałych z przecięcia rury trzema płaszczyznami (w tym dwie równoległe, poziome). Kąt skręcenia osi elips jest obliczony w płaszczyźnie prostopadłej do osi podłużnej rury.
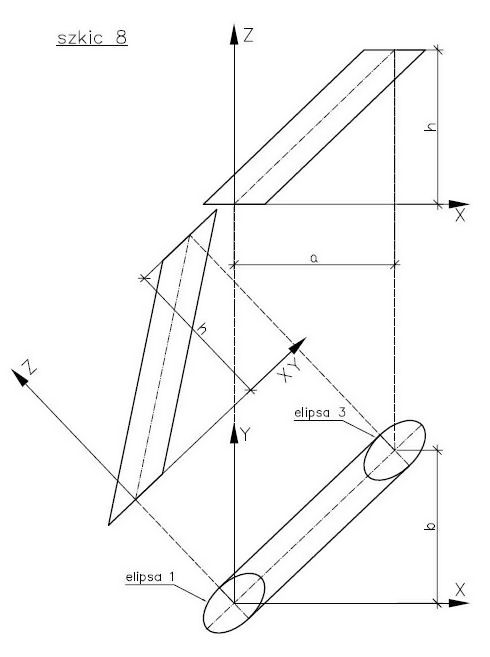
Szkic nr 8 pokazuje usytuowanie rury w przestrzeni oraz wynik cięcia dwoma płaszczyznami poziomymi, gdzie pokazane jest, że powstałe elipsy (elipsa 1 i elipsa 3) są identyczne, a ich osie długie są równoległe i tej samej długości.
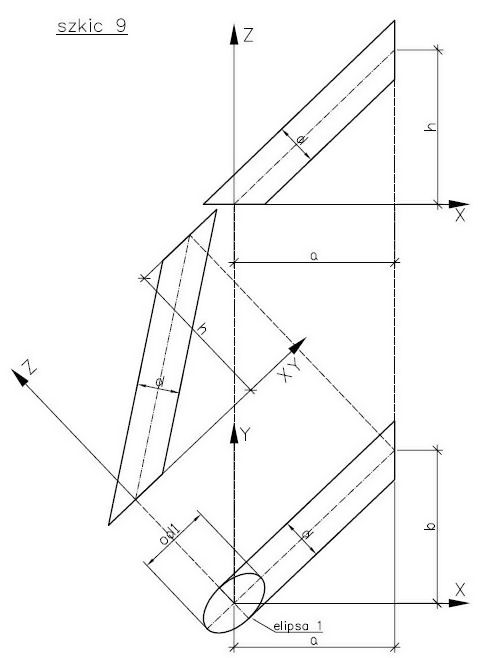
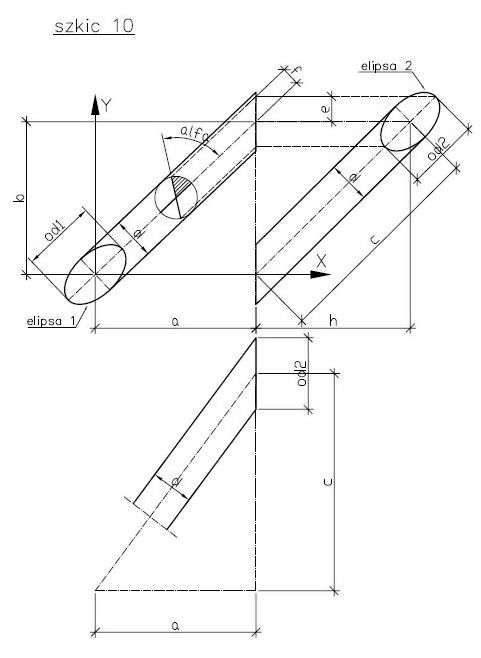
Szkic nr 9 i 10 pokazują konstrukcję niezbędną do wyliczenia kąta skręcenia osi długich elips 1 i 2 w płaszczyźnie prostopadłej do osi podłużnej, oraz pomocnicze parametry jak „c”, „f”, „e”, „od2” wykorzystywane w trakcie obliczania kąta skręcenia, którego wartość jest zależna od wartości danych wyjściowych: „a”, „b”, „h”.
Ostateczny wzór na obliczenie kąta skręcenia:
Alfa = arcsin ( 2*b*Pierw. ((a2+b2+h2)/((a2+b2)*(h2+b2))))
Istotnym w tym wzorze jest też to, że kąta alfa nie zależy od średnicy rury „d”.
Rozwiązanie pokazuje konstrukcję geometryczną niezbędną do obliczenia kąta skręcenia osi długich dwóch elips powstałych z przecięcia rury trzema płaszczyznami (w tym dwie równoległe, poziome). Kąt skręcenia osi elips jest obliczony w płaszczyźnie prostopadłej do osi podłużnej rury.
Szkic nr 8 pokazuje usytuowanie rury w przestrzeni oraz wynik cięcia dwoma płaszczyznami poziomymi, gdzie pokazane jest, że powstałe elipsy (elipsa 1 i elipsa 3) są identyczne, a ich osie długie są równoległe i tej samej długości.
Szkic nr 9 i 10 pokazują konstrukcję niezbędną do wyliczenia kąta skręcenia osi długich elips 1 i 2 w płaszczyźnie prostopadłej do osi podłużnej, oraz pomocnicze parametry jak „c”, „f”, „e”, „od2” wykorzystywane w trakcie obliczania kąta skręcenia, którego wartość jest zależna od wartości danych wyjściowych: „a”, „b”, „h”.
Ostateczny wzór na obliczenie kąta skręcenia:
Alfa = arcsin ( 2*b*Pierw. ((a2+b2+h2)/((a2+b2)*(h2+b2))))
Istotnym w tym wzorze jest też to, że kąta alfa nie zależy od średnicy rury „d”.


MASZYNY DO OBRÓBKI DREWNA
PROJEKTOWANIE KONSTRUKCJI
STALOWYCH ŻELBETOWYCH DREWNIANYCH
PROJEKTOWANIE KONSTRUKCJI
STALOWYCH ŻELBETOWYCH DREWNIANYCH